Categorical variables are pivotal as they often carry essential information that influences the outcome of predictive models. However, their non-numeric nature presents unique challenges in model processing, necessitating specific strategies for encoding. This post will begin by discussing the different types of categorical data often encountered in datasets. We will explore ordinal encoding in-depth and how it can be leveraged when implementing a Decision Tree Regressor. Through practical Python examples using the OrdinalEncoder from sklearn and the Ames Housing dataset, this guide will provide you with the skills to implement these strategies effectively. Additionally, we will visually demonstrate how these encoded variables influence the decisions of a Decision Tree Regressor.
Let’s get started.
Decision Trees and Ordinal Encoding
Photo by Kai Pilger. Some rights reserved.
Overview
This post is divided into three parts; they are:
- Understanding Categorical Variables: Ordinal vs. Nominal
- Implementing Ordinal Encoding in Python
- Visualizing Decision Trees: Insights from Ordinally Encoded Data
Understanding Categorical Variables: Ordinal vs. Nominal
Categorical features in datasets are fundamental elements that need careful handling during preprocessing to ensure accurate model predictions. These features can broadly be classified into two types: ordinal and nominal. Ordinal features possess a natural order or hierarchy among their categories. An example is the feature “ExterQual” in the Ames dataset, which describes the quality of the material on the exterior of a house with levels like “Poor”, “Fair”, “Average”, “Good”, and “Excellent”. The order among these categories is significant and can be utilized in predictive modeling. Nominal features, in contrast, do not imply any inherent order. Categories are distinct and have no order relationship between them. For instance, the “Neighborhood” feature represents various names of neighborhoods like “CollgCr”, “Veenker”, “Crawfor”, etc., without any intrinsic ranking or hierarchy.
The preprocessing of categorical variables is crucial because most machine learning algorithms require input data in numerical format. This conversion from categorical to numerical is typically achieved through encoding. The choice of encoding strategy is pivotal and is influenced by both the type of categorical variable and the model being used.
Encoding Strategies for Machine Learning Models
Linear models, such as linear regression, typically employ one-hot encoding for both ordinal and nominal features. This method transforms each category into a new binary variable, ensuring that the model treats each category as an independent entity without any ordinal relationship. This is essential because linear models assume interval data. That is, linear models interpret numerical input linearly, meaning the numerical value assigned to each category in ordinal encoding could mislead the model. Each incremental integer value in ordinal encoding might be incorrectly assumed by a linear model to reflect an equal step increase in the underlying quantitative measure, which can distort the model output if this assumption doesn’t hold.
Tree-based models, which include algorithms like decision trees and random forests, handle categorical data differently. These models can benefit from ordinal encoding for ordinal features because they make binary splits based on the feature values. The inherent order preserved in ordinal encoding can assist these models in making more effective splits. Tree-based models do not inherently evaluate the arithmetic difference between categories. Instead, they assess whether a particular split at any given encoded value best segments the target variable into its classes or ranges. Unlike linear models, this makes them less sensitive to how the categories are spaced.
Now that we’ve explored the types of categorical variables and their implications for machine learning models, the next part will guide you through the practical application of these concepts. We’ll dive into how to implement ordinal encoding in Python using the Ames dataset, providing you with the tools to efficiently prepare your data for model training.
Implementing Ordinal Encoding in Python
To implement ordinal encoding in Python, we use the OrdinalEncoder from sklearn.preprocessing. This tool is particularly useful for preparing ordinal features for tree-based models. It allows us to specify the order of categories manually, ensuring that the encoding respects the natural hierarchy of the data. We can achieve this using the information in the expanded data dictionary:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
# Import necessary libraries import pandas as pd from sklearn.pipeline import Pipeline from sklearn.impute import SimpleImputer from sklearn.compose import ColumnTransformer from sklearn.preprocessing import FunctionTransformer, OrdinalEncoder
# Load the dataset Ames = pd.read_csv(‘Ames.csv’)
# Manually specify the categories for ordinal encoding according to the data dictionary ordinal_order = { ‘Electrical’: [‘Mix’, ‘FuseP’, ‘FuseF’, ‘FuseA’, ‘SBrkr’], # Electrical system ‘LotShape’: [‘IR3’, ‘IR2’, ‘IR1’, ‘Reg’], # General shape of property ‘Utilities’: [‘ELO’, ‘NoSeWa’, ‘NoSewr’, ‘AllPub’], # Type of utilities available ‘LandSlope’: [‘Sev’, ‘Mod’, ‘Gtl’], # Slope of property ‘ExterQual’: [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Evaluates the quality of the material on the exterior ‘ExterCond’: [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Evaluates the present condition of the material on the exterior ‘BsmtQual’: [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Height of the basement ‘BsmtCond’: [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # General condition of the basement ‘BsmtExposure’: [‘None’, ‘No’, ‘Mn’, ‘Av’, ‘Gd’], # Walkout or garden level basement walls ‘BsmtFinType1’: [‘None’, ‘Unf’, ‘LwQ’, ‘Rec’, ‘BLQ’, ‘ALQ’, ‘GLQ’], # Quality of basement finished area ‘BsmtFinType2’: [‘None’, ‘Unf’, ‘LwQ’, ‘Rec’, ‘BLQ’, ‘ALQ’, ‘GLQ’], # Quality of second basement finished area ‘HeatingQC’: [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Heating quality and condition ‘KitchenQual’: [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Kitchen quality ‘Functional’: [‘Sal’, ‘Sev’, ‘Maj2’, ‘Maj1’, ‘Mod’, ‘Min2’, ‘Min1’, ‘Typ’], # Home functionality ‘FireplaceQu’: [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Fireplace quality ‘GarageFinish’: [‘None’, ‘Unf’, ‘RFn’, ‘Fin’], # Interior finish of the garage ‘GarageQual’: [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Garage quality ‘GarageCond’: [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Garage condition ‘PavedDrive’: [‘N’, ‘P’, ‘Y’], # Paved driveway ‘PoolQC’: [‘None’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], # Pool quality ‘Fence’: [‘None’, ‘MnWw’, ‘GdWo’, ‘MnPrv’, ‘GdPrv’] # Fence quality }
# Extract list of ALL ordinal features from dictionary ordinal_features = list(ordinal_order.keys())
# List of ordinal features except Electrical ordinal_except_electrical = [feature for feature in ordinal_features if feature != ‘Electrical’]
# Specific transformer for ‘Electrical’ using the mode for imputation electrical_imputer = Pipeline(steps=[ (‘impute_electrical’, SimpleImputer(strategy=‘most_frequent’)) ])
# Helper function to fill ‘None’ for other ordinal features def fill_none(X): return X.fillna(“None”)
# Pipeline for ordinal features: Fill missing values with ‘None’ ordinal_imputer = Pipeline(steps=[ (‘fill_none’, FunctionTransformer(fill_none, validate=False)) ])
# Preprocessor for filling missing values preprocessor_fill = ColumnTransformer(transformers=[ (‘electrical’, electrical_imputer, [‘Electrical’]), (‘cat’, ordinal_imputer, ordinal_except_electrical) ])
# Apply preprocessor for filling missing values Ames_ordinal = preprocessor_fill.fit_transform(Ames[ordinal_features])
# Convert back to DataFrame to apply OrdinalEncoder Ames_ordinal = pd.DataFrame(Ames_ordinal, columns=[‘Electrical’] + ordinal_except_electrical)
# Apply Ordinal Encoding categories = [ordinal_order[feature] for feature in ordinal_features] ordinal_encoder = OrdinalEncoder(categories=categories) Ames_ordinal_encoded = ordinal_encoder.fit_transform(Ames_ordinal) Ames_ordinal_encoded = pd.DataFrame(Ames_ordinal_encoded, columns=[‘Electrical’] + ordinal_except_electrical) |
The code block above efficiently handles the preprocessing of categorical variables by first filling missing values and then applying the appropriate encoding strategy. By viewing the dataset before encoding, we can confirm that our preprocessing steps have been correctly applied:
|
# Ames dataset of ordinal features prior to ordinal encoding print(Ames_ordinal) |
|
Electrical LotShape Utilities LandSlope … GarageCond PavedDrive PoolQC Fence 0 SBrkr Reg AllPub Gtl … TA Y None None 1 SBrkr Reg AllPub Gtl … TA Y None None 2 SBrkr Reg AllPub Gtl … Po N None None 3 SBrkr Reg AllPub Gtl … TA N None None 4 SBrkr Reg AllPub Gtl … TA Y None None … … … … … … … … … … 2574 FuseF Reg AllPub Gtl … Po P None None 2575 FuseA IR1 AllPub Gtl … TA Y None None 2576 FuseA Reg AllPub Gtl … TA Y None None 2577 SBrkr Reg AllPub Gtl … TA Y None None 2578 SBrkr IR1 AllPub Gtl … TA Y None None
[2579 rows x 21 columns] |
The output above highlights the ordinal features in the Ames dataset prior to any ordinal encoding. Below, we illustrate the specific information we provide to the OrdinalEncoder. Please note that we do not provide a list of features. We simply provide the ranking of each feature in the order they appear in our dataset.
|
# The information we input into ordinal encoder, it will automatically assign 0, 1, 2, 3, etc. print(categories) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
[[‘Mix’, ‘FuseP’, ‘FuseF’, ‘FuseA’, ‘SBrkr’], [‘IR3’, ‘IR2’, ‘IR1’, ‘Reg’], [‘ELO’, ‘NoSeWa’, ‘NoSewr’, ‘AllPub’], [‘Sev’, ‘Mod’, ‘Gtl’], [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘No’, ‘Mn’, ‘Av’, ‘Gd’], [‘None’, ‘Unf’, ‘LwQ’, ‘Rec’, ‘BLQ’, ‘ALQ’, ‘GLQ’], [‘None’, ‘Unf’, ‘LwQ’, ‘Rec’, ‘BLQ’, ‘ALQ’, ‘GLQ’], [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘Sal’, ‘Sev’, ‘Maj2’, ‘Maj1’, ‘Mod’, ‘Min2’, ‘Min1’, ‘Typ’], [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘Unf’, ‘RFn’, ‘Fin’], [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘Po’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘N’, ‘P’, ‘Y’], [‘None’, ‘Fa’, ‘TA’, ‘Gd’, ‘Ex’], [‘None’, ‘MnWw’, ‘GdWo’, ‘MnPrv’, ‘GdPrv’]] |
This sets the stage for an effective application of ordinal encoding, where the natural ordering of categories is crucial for subsequent model training. Each category within a feature will be converted to a numerical value that reflects its rank or importance as specified, without assuming any equidistant spacing between them.
|
# Ames dataset of ordinal features after ordinal encoding print(Ames_ordinal_encoded) |
The transformed dataset is shown below. It is highly recommended to do a quick check against the original dataset to ensure that the results align with the information we obtained from the data dictionary.
|
Electrical LotShape Utilities … PavedDrive PoolQC Fence 0 4.0 3.0 3.0 … 2.0 0.0 0.0 1 4.0 3.0 3.0 … 2.0 0.0 0.0 2 4.0 3.0 3.0 … 0.0 0.0 0.0 3 4.0 3.0 3.0 … 0.0 0.0 0.0 4 4.0 3.0 3.0 … 2.0 0.0 0.0 … … … … … … … … 2574 2.0 3.0 3.0 … 1.0 0.0 0.0 2575 3.0 2.0 3.0 … 2.0 0.0 0.0 2576 3.0 3.0 3.0 … 2.0 0.0 0.0 2577 4.0 3.0 3.0 … 2.0 0.0 0.0 2578 4.0 2.0 3.0 … 2.0 0.0 0.0
[2579 rows x 21 columns] |
As we conclude this segment on implementing ordinal encoding, we have set the stage for a robust analysis. By meticulously mapping each ordinal feature to its intrinsic hierarchical value, we empower our predictive models to understand better and leverage the structured relationships inherent in the data. The careful attention to the encoding detail paves the way for more insightful and precise modeling.
Visualizing Decision Trees: Insights from Ordinally Encoded Data
In the final part of this post, we’ll delve into how a Decision Tree Regressor interprets and utilizes this carefully encoded data. We will visually explore the decision-making process of the tree, highlighting how the ordinal nature of our features influences the paths and decisions within the model. This visual depiction will not only affirm the importance of correct data preparation but also illuminate the model’s reasoning in a tangible way. With the categorical variables now thoughtfully preprocessed and encoded, our dataset is primed for the next crucial step: training the Decision Tree Regressor:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# Building on the above blocks of code # Import the necessary libraries from sklearn.tree import DecisionTreeRegressor from sklearn.model_selection import train_test_split import dtreeviz
# Load and split the data X_ordinal = Ames_ordinal_encoded # Use only the ordinal features for fitting the model y = Ames[‘SalePrice’] X_train, X_test, y_train, y_test = train_test_split(X_ordinal, y, test_size=0.2, random_state=42)
# Initialize and fit the Decision Tree tree_model = DecisionTreeRegressor(max_depth=3) tree_model.fit(X_train.values, y_train)
# Visualize the decision tree using dtreeviz viz = dtreeviz.model(tree_model, X_train, y_train, target_name=‘SalePrice’, feature_names=X_train.columns.tolist())
# In Jupyter Notebook, you can directly view the visual using the below: # viz.view() # Renders and displays the SVG visualization
# In PyCharm, you can render and display the SVG image: v = viz.view() # render as SVG into internal object v.show() # pop up window |
By visualizing the decision tree, we provide a graphical representation of how our model processes features to arrive at predictions:
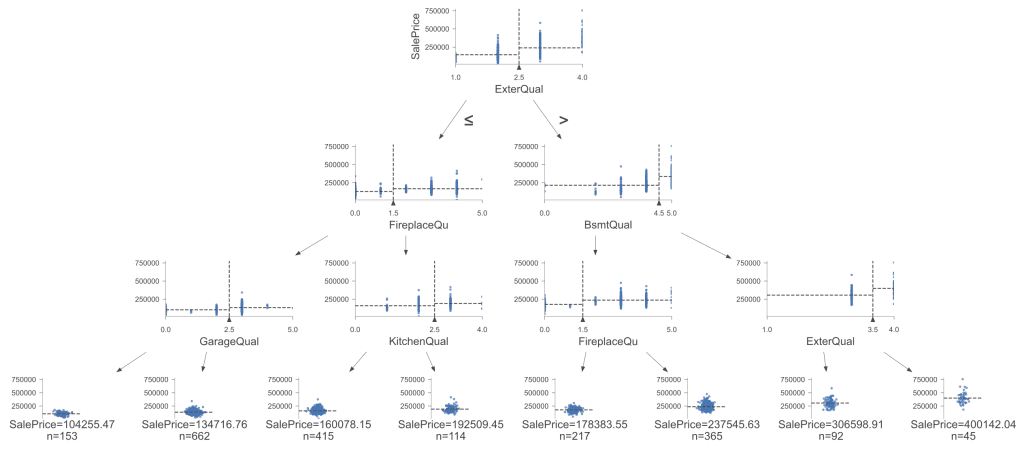
Visualized decision tree. Click to enlarge.
The features chosen for the splits in this tree include ‘ExterQual’, ‘FireplaceQu’, ‘BsmtQual’, and ‘GarageQual’, and ‘KitchenQual’. These features were selected based on their ability to reduce the MSE when used to split the data. The levels or thresholds for these splits (e.g., ExterQual <= 2.5) were determined during the training process to optimize the separation of data points into more homogeneous groups. This visualization not only confirms the efficacy of our encoding strategy but also showcases the strategic depth that decision trees bring to predictive modeling.
Further Reading
APIs
Tutorials
Ames Housing Dataset & Data Dictionary
Summary
In this post, you examined the distinction between ordinal and nominal categorical variables. By implementing ordinal encoding using Python and the OrdinalEncoder from sklearn, you’ve prepared the Ames dataset in a way that respects the inherent order of the data. Finally, you’ve seen firsthand how visualizing decision trees with this encoded data provides tangible insights, offering a clearer perspective on how models predict based on the features you provide.
Specifically, you learned:
- Fundamental Distinctions in Categorical Variables: Understanding the difference between ordinal and nominal variables.
- Model-Specific Preprocessing Needs: Different models, like linear regressor and decision trees, require tailored preprocessing of categorical data to optimize their performance.
- Manual Specification in Ordinal Encoding: The usage of “categories” in the
OrdinalEncoderto customize your encoding strategy.
Do you have any questions? Please ask your questions in the comments below, and I will do my best to answer.
Get Started on The Beginner’s Guide to Data Science!
Learn the mindset to become successful in data science projects
…using only minimal math and statistics, acquire your skill through short examples in Python
Discover how in my new Ebook:
The Beginner’s Guide to Data Science
It provides self-study tutorials with all working code in Python to turn you from a novice to an expert. It shows you how to find outliers, confirm the normality of data, find correlated features, handle skewness, check hypotheses, and much more…all to support you in creating a narrative from a dataset.
Kick-start your data science journey with hands-on exercises
See What’s Inside